
Did you know that linear algebra is super useful in lots of real-life stuff? It helps with things like making computer graphics, analyzing data, and even engineering and secret codes.
In school, learning about linear algebra is important for students studying math, computer science, and engineering. It’s not just for class though—it’s used in jobs too, helping people solve tricky problems in different fields.
Doing hands-on projects with linear algebra is a great way to learn. These projects let you practice what you’ve learned in a fun way, helping you get better at solving problems.
In this blog, we’ll talk about all kinds of linear algebra project ideas. Whether you’re just starting out or already know a bit, we’ve got something for you. Let’s get started!
What is Linear Algebra?
Linear algebra is a branch of mathematics that deals with studying vectors, vector spaces, linear transformations, and systems of linear equations.
In simpler terms, it’s a way of using math to understand and work with things like lines, planes, and spaces in multiple dimensions.
It’s used in various fields like computer science, engineering, physics, economics, and more to solve problems involving patterns, relationships, and transformations.
Benefits of Linear Algebra Projects for Students
Engaging in linear algebra projects offers several benefits for students:
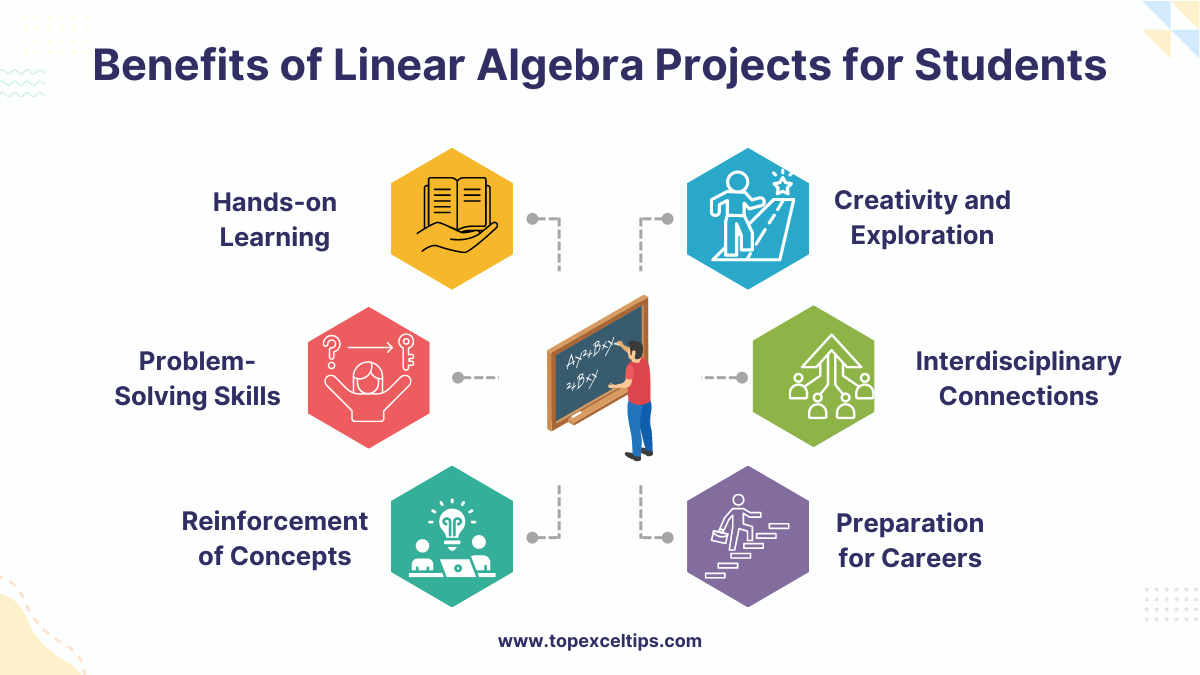
1. Hands-on Learning
Projects provide a practical way for students to apply theoretical concepts learned in class to real-world scenarios. This hands-on approach enhances understanding and retention of material.
2. Problem-Solving Skills
Working on projects encourages critical thinking and problem-solving skills. Students learn to analyze problems, devise strategies, and implement solutions, fostering a deeper understanding of mathematical concepts.
3. Reinforcement of Concepts
Projects reinforce learning by allowing students to explore and experiment with concepts independently. This active participation helps solidify understanding and builds confidence in applying mathematical principles.
4. Creativity and Exploration
Projects encourage creativity and exploration as students design their approaches to solving problems. This freedom allows for personalization and fosters a deeper appreciation for the subject.
5. Interdisciplinary Connections
Linear algebra projects often intersect with other disciplines, such as computer science, physics, and engineering. Engaging in such projects fosters interdisciplinary connections and highlights the practical applications of linear algebra in various fields.
6. Preparation for Careers
Experience with linear algebra projects equips students with valuable skills applicable in academic and professional settings. These skills include data analysis, modeling, programming, and problem-solving, enhancing their readiness for future careers in STEM fields.
Interesting Linear Algebra Project Ideas for Basic to Advanced Level
Linear algebra offers a wide range of interesting project ideas that can cater to various skill levels. Here are some ideas ranging from basic to advanced:
Basic Linear Algebra Projects
#1. Vector Operations Visualizer
Create a program that allows users to input vectors and perform basic operations like addition, subtraction, and scalar multiplication. Visualize the results graphically to deepen your understanding of vector operations.
What Makes This Project?
- Interactive graphical visualization.
- User-friendly interface for vector manipulation.
- Clear depiction of vector arithmetic concepts.
#2. Matrix Calculator
Develop a tool that enables users to input matrices and perform operations such as addition, subtraction, multiplication, and finding determinants. Include functionalities to solve systems of linear equations.
What Makes This Project?
- Comprehensive matrix operation capabilities.
- Simple input and output functionalities.
- Efficient solution for linear algebra computations.
#3. Linear Transformation Simulator
Build an interactive simulator to demonstrate linear transformations such as rotations, scaling, and shearing in 2D or 3D space. Allow users to input transformation matrices and visualize the effects on geometric shapes.
What Makes This Project?
- Dynamic visual representation of transformations.
- Intuitive controls for matrix input.
- An insightful exploration of geometric concepts.
#4. Eigenvalue and Eigenvector Finder
Design a program that computes eigenvalues and eigenvectors of square matrices. Provide explanations and visualizations to illustrate the significance of eigenvalues and eigenvectors in understanding transformations.
What Makes This Project?
- Accurate computation of eigenvalues/eigenvectors.
- Clear explanations of eigenvalue significance.
- Visual aids for understanding transformations.
#5. Least Squares Regression Analyzer
Develop a tool to perform linear regression analysis using the least squares method. Allow users to input datasets and visualize the regression line, providing insights into modeling relationships between variables.
What Makes This Project?
- Robust analysis tool for regression modeling.
- User-friendly interface for dataset input.
- Insightful visualization of regression results.
#6. Linear Algebra Puzzle Solver
Create a series of puzzles or challenges based on linear algebra concepts such as matrix manipulation, solving systems of equations, or finding eigenvalues. Offer hints and explanations to guide users through solving each puzzle.
What Makes This Project?
- Engaging challenges based on linear algebra.
- Interactive hints and explanations were provided.
- Fun and educational problem-solving experience.
Intermediate Linear Algebra Projects
#7. Image Compression Using Singular Value Decomposition (SVD)
Implement an image compression algorithm based on SVD. Explore how reducing the rank of the image matrix affects image quality and file size, demonstrating the power of SVD in data compression.
What Makes This Project?
- Efficient compression with SVD.
- Retains image quality effectively.
- Demonstrates SVD’s practical applications.
#8. Principal Component Analysis (PCA) for Dimensionality Reduction
Develop a PCA algorithm to reduce the dimensionality of high-dimensional datasets while preserving key information. Apply PCA to real-world datasets and visualize the reduced dimensions for analysis.
What Makes This Project?
- Effective high-dimensional data analysis.
- Preserves essential data features.
- Insightful visualization of data reduction.
#9. Markov Chain Analysis and PageRank Algorithm
Analyze a network using Markov chains and implement the PageRank algorithm to rank web pages based on importance. Explore the linear algebra behind PageRank and its application in search engine algorithms.
What Makes This Project?
- Understand web page importance ranking.
- Applies linear algebra to web analysis.
- Practical implementation of PageRank algorithm.
#10. Linear Regression with Regularization Techniques
Extend basic linear regression by implementing regularization techniques such as Lasso and Ridge regression. Compare the performance of different regularization methods on datasets with varying complexities.
What Makes This Project?
- Improves regression model accuracy.
- Handles multicollinearity and overfitting.
- Explores advanced regression techniques.
#11. Finite Element Method (FEM) Simulation
Create a simulation tool using FEM to solve partial differential equations (PDEs). Apply FEM to model physical phenomena like heat transfer or structural analysis, emphasizing the linear algebra computations involved.
What Makes This Project?
- Accurate modeling of physical phenomena.
- Utilizes linear algebra in simulation.
- Real-world applications in engineering.
#12. Optimization Problems with Linear Programming
Formulate optimization problems using linear programming techniques. Implement algorithms to solve linear programming problems and apply them to real-world scenarios like resource allocation or production planning.
What Makes This Project?
- Solves complex resource allocation problems.
- Efficiently handles production planning challenges.
- Practical implementation of linear programming.
Advanced Linear Algebra Projects
#13. Tensor Decomposition for Multidimensional Data Analysis
Develop algorithms for tensor decomposition to analyze multidimensional data. Apply techniques like Tucker decomposition or CP decomposition to extract meaningful patterns and structures from complex datasets.
What Makes This Project?
- Unveils intricate data patterns efficiently.
- Handles high-dimensional data effectively.
- Enables insights into complex datasets.
#14. Graph Spectral Analysis and Community Detection
Implement spectral graph theory algorithms to analyze network structures. Explore methods like spectral clustering and modularity optimization for community detection in large-scale networks.
What Makes This Project?
- Reveals network structures with precision.
- Identifies cohesive communities within networks.
- Applies advanced graph theory algorithms.
#15. Non-negative Matrix Factorization (NMF) for Topic Modeling
Build an NMF-based topic modeling system to extract topics from text corpora. Apply NMF to uncover latent topics in documents and visualize topic distributions for analysis and interpretation.
What Makes This Project?
- Extracts interpretable topics from text data.
- Utilizes advanced matrix factorization techniques.
- Enhances understanding of document collections.
#16. Kernel Methods for Nonlinear Dimensionality Reduction
Explore kernel methods like kernel PCA and kernel t-SNE for nonlinear dimensionality reduction. Apply these techniques to high-dimensional datasets to uncover nonlinear relationships and patterns.
What Makes This Project?
- Uncovers nonlinear patterns in high dimensions.
- Employs sophisticated kernel-based techniques.
- Offers insights beyond linear methods.
#17. Advanced Signal Processing Using Wavelet Transform
Develop signal processing algorithms based on wavelet transforms. Apply wavelet analysis to denoise signals, detect features, and extract time-frequency information from complex signals such as audio and biomedical data.
What Makes This Project?
- Captures intricate signal features accurately.
- Analyzes signals in the time-frequency domain.
- Enhances signal processing capabilities significantly.
#18. Quantum Computing and Quantum Linear Algebra
Dive into the principles of quantum linear algebra and quantum computing. Explore quantum algorithms for linear algebraic problems such as matrix inversion, solving systems of linear equations, and quantum state preparation.
What Makes This Project?
- Explores cutting-edge quantum computing principles.
- Applies quantum algorithms to linear algebra.
- Pushes boundaries of computational capabilities.
Prerequisites for Linear Algebra Projects
Here are some prerequisites for engaging in linear algebra projects:
1. Basic Mathematics Knowledge:
- Understanding of arithmetic operations, algebraic expressions, and basic geometry.
- Familiarity with concepts like equations, functions, and graphs.
2. Fundamental Linear Algebra Concepts:
- Knowledge of vectors, matrices, and their operations (addition, multiplication).
- Understanding of vector spaces, linear transformations, and eigenvalues/eigenvectors.
3. Algebraic Manipulation Skills:
- Ability to manipulate algebraic expressions, solve equations, and perform matrix calculations.
- Understanding of properties of matrices and vectors.
4. Programming Skills (depending on the project):
- Proficiency in programming languages like Python, MATLAB, or R for implementing algorithms and visualizations.
- Understanding of basic programming constructs such as loops, conditionals, and functions.
5. Critical Thinking and Problem-Solving Skills:
- Capacity to analyze problems, formulate strategies, and apply mathematical concepts to solve them.
- Ability to think logically and creatively to tackle complex problems.
6. Interest and Motivation:
- Enthusiasm for exploring mathematical concepts and their applications.
- Willingness to engage in hands-on projects and learn through practical experience.
Tips for Successful Linear Algebra Projects
Here are some tips for successful linear algebra projects:
1. Understand the Problem
Take time to thoroughly understand the problem statement or objective of your project. Clarify any ambiguities and ensure you grasp the underlying concepts involved.
2. Plan Your Approach
Develop a clear plan or strategy for tackling the project. Break down the problem into manageable steps and outline the methods or algorithms you intend to use.
3. Utilize Resources
Make use of textbooks, online resources, and other reference materials to deepen your understanding of relevant linear algebra concepts. Seek guidance from instructors, peers, or online communities if needed.
4. Implement Algorithms
Write clear and efficient code to implement algorithms or mathematical operations required for your project. Test your code rigorously to ensure correctness and reliability.
5. Visualize Results
Use visualizations, plots, and diagrams to illustrate your findings and enhance understanding. Visual representations can help communicate complex ideas more effectively.
6. Document Your Work
Maintain detailed documentation of your project, including your approach, methods, code, results, and any insights gained. Documentation aids in understanding, troubleshooting, and presenting your work to others.
7. Iterate and Improve
Be prepared to iterate on your project, refining your methods and making improvements based on feedback or new insights. Continuously seek opportunities to enhance the quality and effectiveness of your work.
8. Stay Organized
Keep your project files, code, and documentation well-organized and structured. This helps streamline your workflow and makes it easier to navigate and manage your project components.
9. Stay Engaged and Curious
Stay curious and engaged throughout the project. Explore related topics, ask questions, and be open to new ideas and approaches. A curious mindset fosters creativity and innovation.
10. Reflect and Learn
Take time to reflect on your project experience and what you’ve learned. Identify areas of strength and areas for improvement, and use these insights to inform future projects or learning endeavors.
Final Words
Linear algebra project ideas offer a dynamic avenue for exploring the practical applications and theoretical foundations of this fundamental branch of mathematics.
From basic concepts to advanced techniques, these projects provide invaluable opportunities for hands-on learning, problem-solving, and creativity.
By engaging in linear algebra projects, students and enthusiasts can deepen their understanding, hone their skills, and gain insights into the diverse applications of linear algebra across various fields.
Whether pursuing simple visualizations or tackling complex computational challenges, the journey through linear algebra projects is not only educational but also enriching, inspiring a deeper appreciation for the beauty and utility of mathematical concepts in the world around us.
Frequently Asked Questions (FAQs)
1. Why is linear algebra important in machine learning?
Linear algebra provides the foundation for many machine learning algorithms, such as matrix factorization, dimensionality reduction, and neural networks.
2. Can beginners undertake advanced linear algebra projects?
While beginners may find advanced projects challenging, they can gradually build their skills by starting with basic and intermediate projects before progressing to more advanced ones.
3. What programming languages are commonly used for linear algebra projects?
Python is widely used for linear algebra projects due to its extensive libraries like NumPy and SciPy, which offer efficient implementations of linear algebra operations.
4. Are there online resources for learning linear algebra project ideas?
Yes, platforms like GitHub, Kaggle, and Coursera offer a plethora of project ideas, tutorials, and datasets for exploring linear algebra concepts.


